
 Legionnaires' disease GIS Tool (ECDC)
Legionnaires' disease GIS Tool (ECDC)
 Legionnaires' disease GIS Tool (ECDC)
Legionnaires' disease GIS Tool (ECDC)
|
Model 1: Case density Model 2: Disease risk Model 3: Buffer density Model 4: Buffer risk |
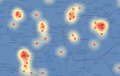
|
